线性代数核心
从基础向量空间到大模型中的矩阵计算,探索线性代数在现代人工智能中的应用与实现
向量空间基础
向量空间是线性代数的基础概念,它是一组向量的集合,满足加法封闭性和标量乘法封闭性。
向量空间的八大性质:
- 加法封闭性
- 加法结合律
- 加法零元素存在
- 加法逆元素存在
- 加法交换律
- 标量乘法封闭性
- 标量乘法分配律
- 标量乘法结合律
常见的向量空间:
- Rn: n维实数向量空间
- Cn: n维复数向量空间
- Pn: n阶多项式空间
- Mm×n: m×n矩阵空间
子空间与基的概念
向量空间的子集如果也构成一个向量空间,则称为子空间。线性无关向量组中的向量数量等于空间维数时,该向量组构成该空间的一组基。
Python示例:验证向量组是否线性相关
import numpy as np
def is_linearly_independent(vectors):
"""检查向量组是否线性无关"""
matrix = np.vstack(vectors)
# 计算矩阵的秩
rank = np.linalg.matrix_rank(matrix)
# 如果秩等于向量数量,则线性无关
return rank == len(vectors)
# 示例向量组
vectors = [
np.array([1, 0, 0]),
np.array([0, 1, 0]),
np.array([0, 0, 1])
]
print(f"向量组是否线性无关: {is_linearly_independent(vectors)}")
# 输出: 向量组是否线性无关: True矩阵运算
矩阵是线性代数中的核心数据结构,通过矩阵运算可以高效地表示和处理线性变换。
基本矩阵运算
矩阵乘法
两个矩阵相乘时,第一个矩阵的列数必须等于第二个矩阵的行数。
矩阵求逆
矩阵A的逆矩阵A-1满足:A·A-1 = A-1·A = I
只有方阵且行列式不为零时才存在逆矩阵
Python中使用NumPy实现矩阵操作
import numpy as np
# 创建两个矩阵
A = np.array([[3, 1], [1, 2]])
B = np.array([[2, 1], [1, 3]])
# 矩阵乘法
C = np.dot(A, B)
print("矩阵乘法结果:\n", C)
# 计算矩阵的行列式
det_A = np.linalg.det(A)
print(f"行列式值: {det_A}")
# 计算矩阵的逆
if det_A != 0:
A_inv = np.linalg.inv(A)
print("矩阵的逆:\n", A_inv)
# 验证逆矩阵性质
identity = np.dot(A, A_inv)
print("A·A^-1:\n", np.round(identity, decimals=10)) # 四舍五入处理浮点误差
else:
print("矩阵不可逆")特征值分解
特征值分解是矩阵分析中的关键工具,它将矩阵分解为由其特征值和特征向量表示的形式。
特征值和特征向量
对于一个n×n方阵A,如果存在一个非零向量v和一个标量λ,使得:
则λ称为A的特征值,v称为A对应于λ的特征向量。
特征值的计算
特征值可以通过求解特征方程得到:
其中I是单位矩阵,det表示行列式。
特征值分解的意义
若n×n矩阵A有n个线性无关的特征向量,则A可以分解为:
其中P是由特征向量组成的矩阵,D是由特征值组成的对角矩阵。特征值分解使得我们可以:
- 计算矩阵的幂:Ak = PDkP-1
- 分析动态系统的稳定性
- 理解主成分分析(PCA)的数学基础
- 识别矩阵代表的变换的主轴和缩放因子
特征值分解的Python实现
import numpy as np
import matplotlib.pyplot as plt
# 创建一个对称矩阵
A = np.array([[4, 2], [2, 3]])
# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)
print("特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)
# 验证分解结果
P = eigenvectors
D = np.diag(eigenvalues)
P_inv = np.linalg.inv(P)
# 重建原矩阵
A_reconstructed = np.dot(np.dot(P, D), P_inv)
print("重建的矩阵:\n", np.round(A_reconstructed, decimals=10))
# 验证特征向量与特征值的关系
for i in range(len(eigenvalues)):
v = eigenvectors[:, i]
Av = np.dot(A, v)
lambda_v = eigenvalues[i] * v
print(f"验证特征向量 {i+1}:")
print(f"A·v = {Av}")
print(f"λ·v = {lambda_v}")
print(f"误差: {np.linalg.norm(Av - lambda_v)}\n")SVD分解及应用
奇异值分解(SVD)是一种强大的矩阵分解方法,它可以应用于任何矩阵,不仅限于方阵。
SVD的定义
对于任意m×n矩阵A,都可以分解为:
其中:
- U是m×m正交矩阵,列向量称为左奇异向量
- Σ是m×n对角矩阵,对角线上的元素是奇异值
- VT是n×n正交矩阵的转置,V的列向量称为右奇异向量
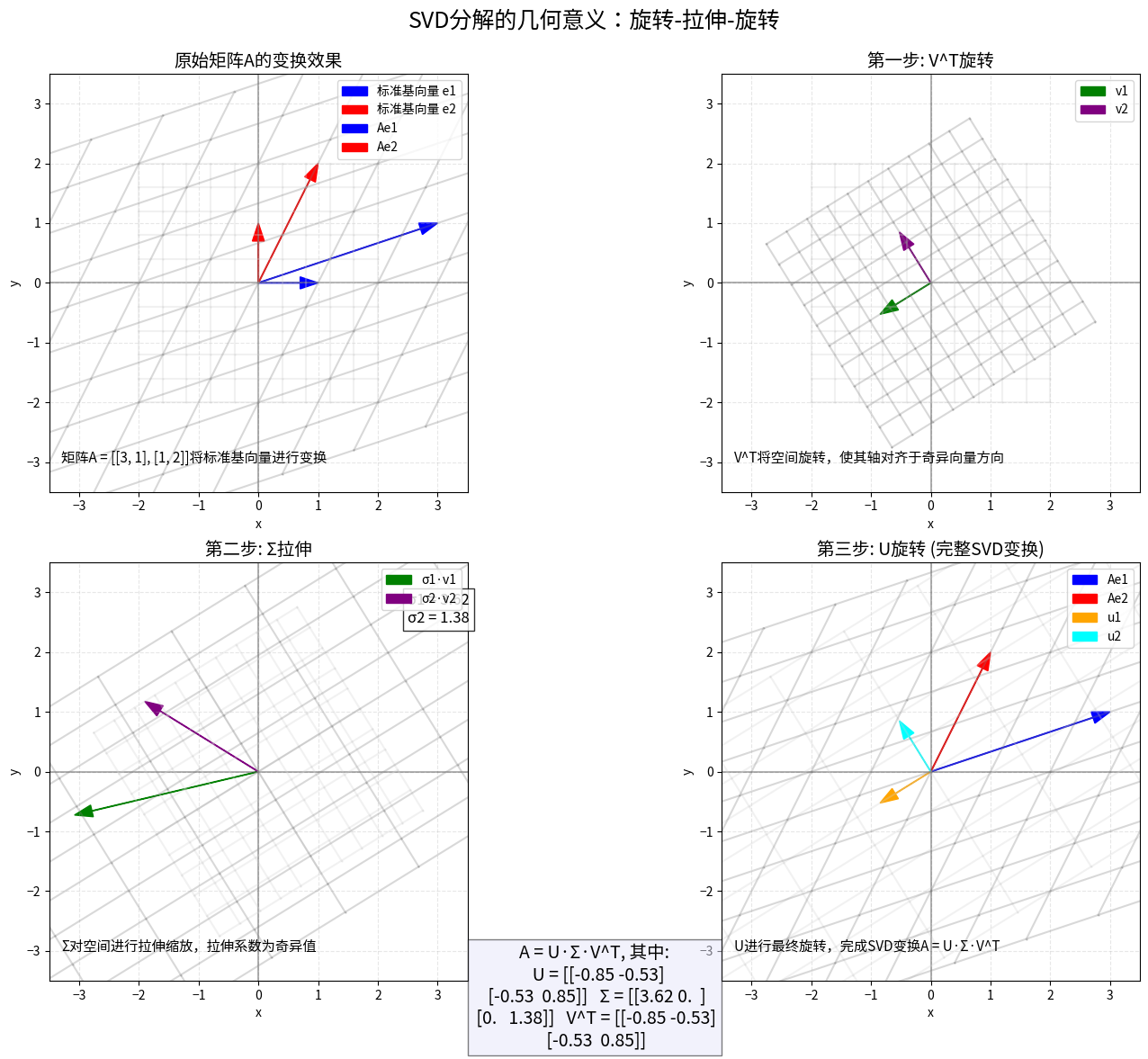
SVD分解的几何意义:旋转-拉伸-旋转变换
SVD在AI中的应用
主成分分析(PCA)
PCA通过SVD找出数据方差最大的方向,从而实现降维。
图像压缩
通过保留最大的奇异值及其对应的奇异向量,可以用较少的数据重构原始图像。
推荐系统
在协同过滤中,SVD可以揭示用户-项目矩阵中的隐藏特征。
噪声过滤
去除小奇异值对应的成分可以有效过滤数据中的噪声。
大模型中的注意力机制与矩阵计算
注意力机制是现代大型语言模型的核心,它使模型能够关注输入序列中的不同部分,从而捕捉上下文关系。
注意力机制的核心组件
注意力机制的核心是通过查询(Q)、键(K)和值(V)三个矩阵的交互来计算权重并获取上下文相关信息。
自注意力计算公式
其中dk是键向量的维度,除以√dk是为了控制点积的数量级。
多头注意力机制
多头注意力通过并行计算多组不同的注意力,使模型能够同时关注不同位置的信息并捕捉不同类型的依赖关系:
- 将Q、K、V分别投影到h个不同的子空间
- 在每个子空间独立计算注意力
- 将h个注意力输出拼接并再次投影
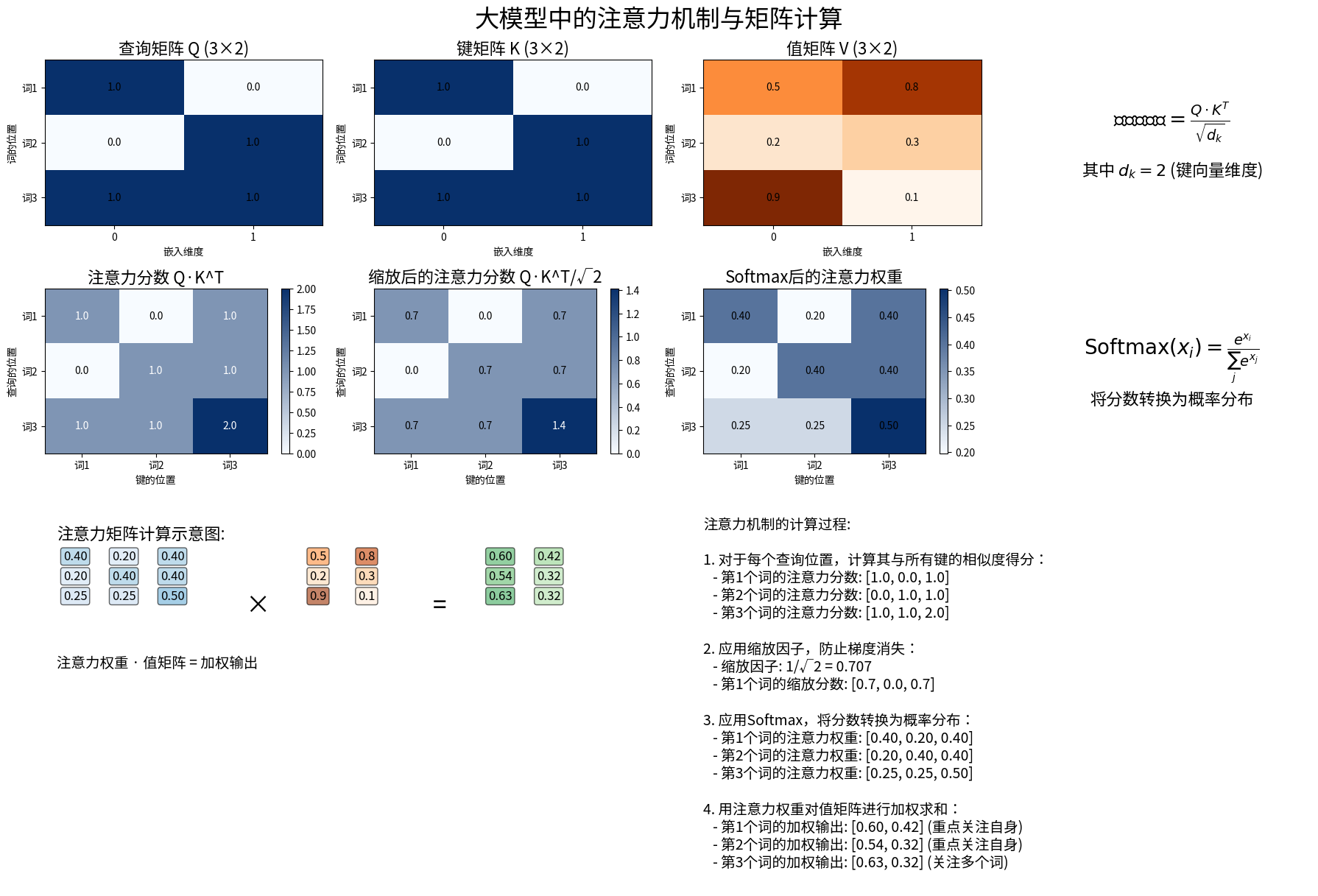
注意力机制的矩阵计算过程
Python实现注意力机制
import numpy as np
def scaled_dot_product_attention(Q, K, V):
"""
计算缩放点积注意力
参数:
Q: 查询矩阵,形状 (seq_len, d_k)
K: 键矩阵,形状 (seq_len, d_k)
V: 值矩阵,形状 (seq_len, d_v)
返回:
注意力加权后的值,形状 (seq_len, d_v)
"""
# 计算注意力分数
d_k = K.shape[1]
scores = np.dot(Q, K.T) / np.sqrt(d_k)
# 应用softmax获取注意力权重
attention_weights = softmax(scores)
# 加权求和
output = np.dot(attention_weights, V)
return output, attention_weights
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
# 为了数值稳定性,减去每行的最大值
exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
return exp_x / np.sum(exp_x, axis=1, keepdims=True)
# 示例输入
seq_len = 3
d_k = 2
d_v = 2
Q = np.array([[1, 0], [0, 1], [1, 1]]) # (3, 2)
K = np.array([[1, 0], [0, 1], [1, 1]]) # (3, 2)
V = np.array([[0.5, 0.8], [0.2, 0.3], [0.9, 0.1]]) # (3, 2)
output, attention_weights = scaled_dot_product_attention(Q, K, V)
print("注意力权重:\n", attention_weights)
print("\n注意力输出:\n", output)图像变换的数学模型
图像变换如旋转、缩放等,可以通过矩阵变换来实现,这是计算机图形学中的基础应用。
常见的图像变换矩阵
平移变换
将图像在二维平面上移动
旋转变换
将图像绕原点旋转θ角度
缩放变换
在x和y方向分别缩放sx和sy倍
切变变换
在x和y方向进行切变
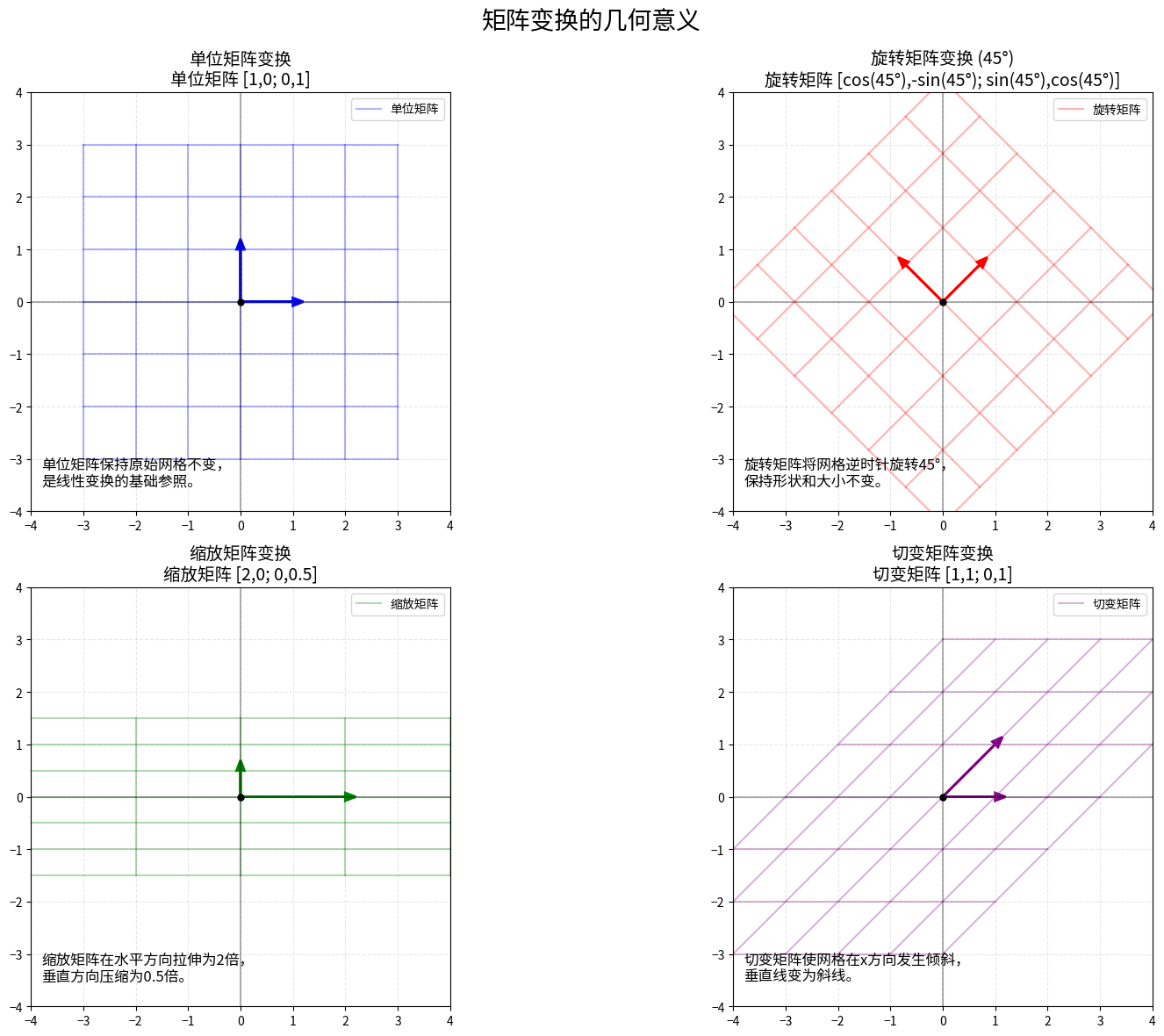
矩阵变换的几何意义图示
齐次坐标系
图像变换通常使用齐次坐标来表示,这样可以将平移、旋转、缩放等变换统一为矩阵乘法操作。使用3×3矩阵表示2D变换,或4×4矩阵表示3D变换。
在齐次坐标中,2D点(x,y)表示为(x,y,1),变换后的坐标为变换矩阵与原坐标的乘积。
Python实现图像变换
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
def transform_point(point, matrix):
"""应用变换矩阵到点"""
# 将2D点转换为齐次坐标
homogeneous_point = np.array([point[0], point[1], 1])
# 应用变换
transformed = np.dot(matrix, homogeneous_point)
# 转回2D坐标
return transformed[:2]
def transform_polygon(vertices, matrix):
"""应用变换矩阵到多边形的所有顶点"""
return np.array([transform_point(v, matrix) for v in vertices])
# 创建一个简单的正方形
square = np.array([[0, 0], [1, 0], [1, 1], [0, 1]])
# 定义不同的变换矩阵
# 旋转45度
theta = np.radians(45)
rotation_matrix = np.array([
[np.cos(theta), -np.sin(theta), 0],
[np.sin(theta), np.cos(theta), 0],
[0, 0, 1]
])
# 缩放: x方向2倍,y方向0.5倍
scaling_matrix = np.array([
[2, 0, 0],
[0, 0.5, 0],
[0, 0, 1]
])
# 平移: x方向1单位,y方向2单位
translation_matrix = np.array([
[1, 0, 1],
[0, 1, 2],
[0, 0, 1]
])
# 切变: x方向切变因子0.5
shear_matrix = np.array([
[1, 0.5, 0],
[0, 1, 0],
[0, 0, 1]
])
# 应用变换
rotated_square = transform_polygon(square, rotation_matrix)
scaled_square = transform_polygon(square, scaling_matrix)
translated_square = transform_polygon(square, translation_matrix)
sheared_square = transform_polygon(square, shear_matrix)
# 绘图
plt.figure(figsize=(12, 10))
plt.subplot(221)
plt.gca().add_patch(Polygon(square, fill=False, edgecolor='blue', label='原始'))
plt.gca().add_patch(Polygon(rotated_square, fill=False, edgecolor='red', label='旋转45°'))
plt.title('旋转变换')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.subplot(222)
plt.gca().add_patch(Polygon(square, fill=False, edgecolor='blue', label='原始'))
plt.gca().add_patch(Polygon(scaled_square, fill=False, edgecolor='green', label='缩放'))
plt.title('缩放变换 (x: 2倍, y: 0.5倍)')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.subplot(223)
plt.gca().add_patch(Polygon(square, fill=False, edgecolor='blue', label='原始'))
plt.gca().add_patch(Polygon(translated_square, fill=False, edgecolor='purple', label='平移'))
plt.title('平移变换 (x: +1, y: +2)')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.subplot(224)
plt.gca().add_patch(Polygon(square, fill=False, edgecolor='blue', label='原始'))
plt.gca().add_patch(Polygon(sheared_square, fill=False, edgecolor='orange', label='切变'))
plt.title('切变变换 (x方向切变因子: 0.5)')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()使用Manim进行线性代数可视化
Manim是一个由3Blue1Brown创建的Python动画库,专为创建数学教育视频而设计,特别适合可视化线性代数概念。
Manim的核心功能
- 创建高质量的数学动画
- 可视化向量、矩阵变换等抽象概念
- 支持复杂的数学符号和公式
- 可编程控制动画过程
- 提供丰富的几何图形和变换效果
安装Manim
# 使用pip安装
pip install manim
# 或者使用conda安装
conda install -c conda-forge manim使用Manim可视化线性变换
from manim import *
class LinearTransformationExample(LinearTransformationScene):
def __init__(self, **kwargs):
LinearTransformationScene.__init__(
self,
include_background_plane=True,
include_foreground_plane=True,
foreground_plane_kwargs={
"x_range": [-8, 8, 1],
"y_range": [-5, 5, 1],
"faded_line_ratio": 0
},
background_plane_kwargs={
"color": BLUE_D,
"axis_config": {
"color": GREEN,
},
"background_line_style": {
"stroke_color": BLUE_E,
"stroke_width": 1,
}
},
**kwargs
)
def construct(self):
# 添加标题
title = Title("线性变换的可视化")
self.add_foreground_mobject(title)
# 展示单位矩阵变换
matrix_tex = MathTex("A = \\begin{bmatrix} 1 & 0 \\\\ 0 & 1 \\end{bmatrix}")
matrix_tex.to_corner(UL).shift(DOWN + RIGHT)
self.add_foreground_mobject(matrix_tex)
self.wait(1)
self.apply_matrix([[1, 0], [0, 1]])
self.wait(1)
# 旋转矩阵变换
matrix_tex.become(
MathTex("A = \\begin{bmatrix} \\cos(45°) & -\\sin(45°) \\\\ \\sin(45°) & \\cos(45°) \\end{bmatrix}")
)
self.wait(1)
self.apply_matrix(
[[np.cos(PI/4), -np.sin(PI/4)],
[np.sin(PI/4), np.cos(PI/4)]]
)
self.wait(1)
# 缩放矩阵变换
matrix_tex.become(
MathTex("A = \\begin{bmatrix} 2 & 0 \\\\ 0 & 0.5 \\end{bmatrix}")
)
self.wait(1)
self.apply_matrix([[2, 0], [0, 0.5]])
self.wait(1)
# 切变矩阵变换
matrix_tex.become(
MathTex("A = \\begin{bmatrix} 1 & 1 \\\\ 0 & 1 \\end{bmatrix}")
)
self.wait(1)
self.apply_matrix([[1, 1], [0, 1]])
self.wait(2)总结与实践建议
核心概念总结
- 向量空间是理解线性代数的基础,掌握其八大性质是必要的
- 矩阵运算是线性代数应用的核心,特别是乘法、求逆和分解操作
- 特征值分解帮助我们理解矩阵的本质特性和变换效果
- SVD分解是应用最广泛的矩阵分解方法,尤其在数据科学和AI领域
- 注意力机制是现代大模型的核心,深入了解其矩阵计算过程有助于理解AI工作原理
- 图像变换是线性代数在计算机图形学中的直观应用
学习路线建议
- 首先掌握向量空间的基本概念
- 理解矩阵的基本运算和性质
- 学习特征值分解及其应用
- 深入理解SVD及其在数据分析中的应用
- 结合NumPy等工具实现各种矩阵操作
- 通过Manim等工具可视化线性变换,加深理解
- 探索线性代数在AI和图形学中的应用
实践项目建议
- 手工实现矩阵乘法和求逆,并与NumPy结果比较
- 使用SVD实现简单的图像压缩程序
- 构建一个基于矩阵变换的图像处理应用
- 使用Python实现简化版的注意力机制
- 创建Manim动画来可视化各种线性变换